
函數(shù) 在
在 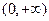 上不單調(diào),則的
上不單調(diào),則的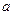 取值范圍是__________.
取值范圍是__________.


函數(shù) 在
在 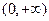 上不單調(diào),則的
上不單調(diào),則的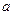 取值范圍是__________.
取值范圍是__________.

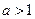
導數(shù)和函數(shù)的單調(diào)性的關系:
(1)若f′(x)>0在(a,b)上恒成立,則f(x)在(a,b)上是增函數(shù),f′(x)>0的解集與定義域的交集的對應區(qū)間為增區(qū)間;
(2)若f′(x)<0在(a,b)上恒成立,則f(x)在(a,b)上是減函數(shù),f′(x)<0的解集與定義域的交集的對應區(qū)間為減區(qū)間。
函數(shù)的單調(diào)性與導數(shù)的關系的知識擴展
1.導數(shù)和函數(shù)的單調(diào)性的關系:
(1)若f′(x)>0在(a,b)上恒成立,則f(x)在(a,b)上是增函數(shù),f′(x)>0的解集與定義域的交集的對應區(qū)間為增區(qū)間;
(2)若f′(x)<0在(a,b)上恒成立,則f(x)在(a,b)上是減函數(shù),f′(x)<0的解集與定義域的交集的對應區(qū)間為減區(qū)間。
2.利用導數(shù)求解多項式函數(shù)單調(diào)性的一般步驟:
①確定f(x)的定義域;
②計算導數(shù)f′(x);
③求出f′(x)=0的根;
④用f′(x)=0的根將f(x)的定義域分成若干個區(qū)間,列表考察這若干個區(qū)間內(nèi)f′(x)的符號,進而確定f(x)的單調(diào)區(qū)間:f′(x)>0,則f(x)在對應區(qū)間上是增函數(shù),對應區(qū)間為增區(qū)間;f′(x)<0,則f(x)在對應區(qū)間上是減函數(shù),對應區(qū)間為減區(qū)間。
查看答案
單次付費有效 3.99 元
用于查看答案,單次有效 19.99元
包月VIP 9.99 元
用于查看答案,包月VIP無限次 49.99元